Research
Quantum Simulation
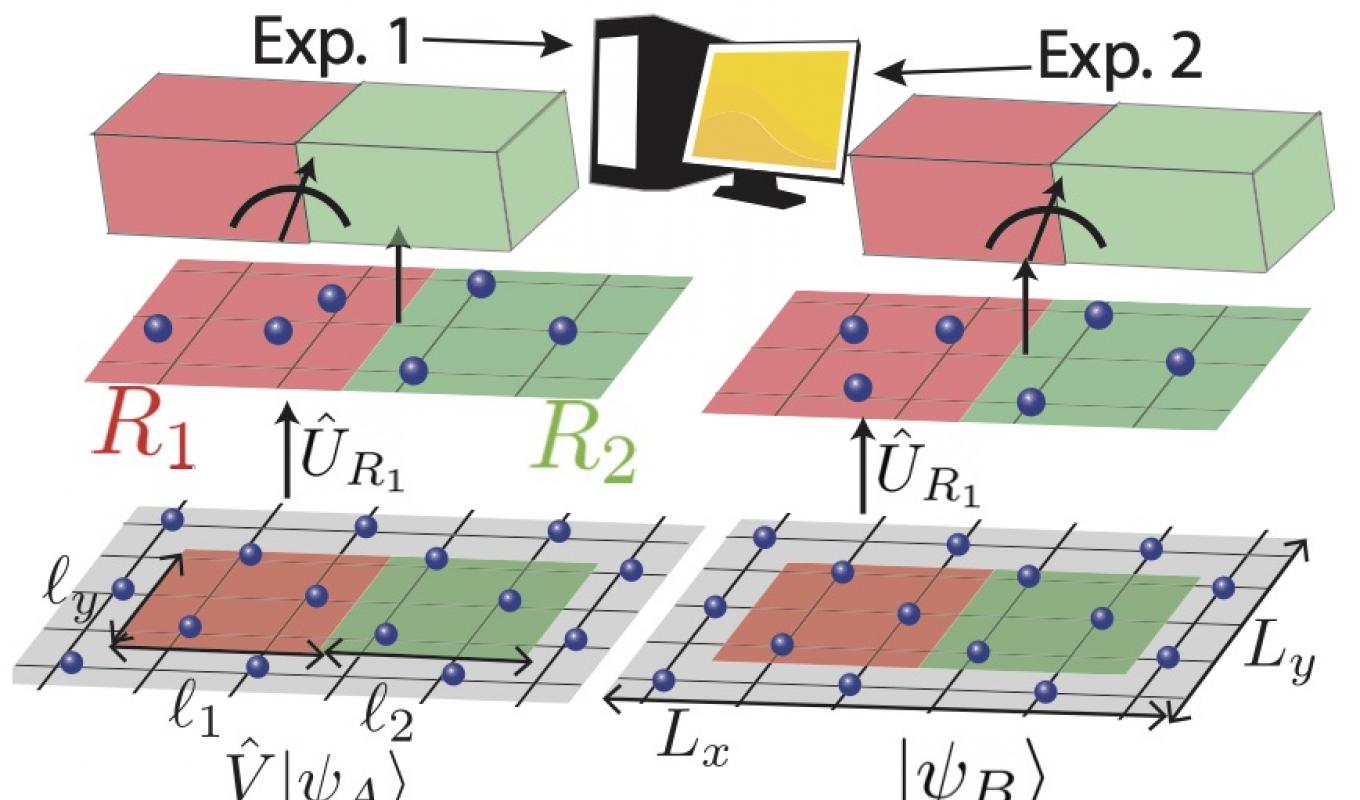
Given the slow but steady rise of quantum simulators, what are the hardware-efficient ways to implement chemical and physical models? How can we verify that we have implemented the right Hamiltonian? How can we efficiently characterize many-body states on such systems and measure them? Any quantum system is noisy, how can we find efficient ways to characterize and combat the noise?
Quantum optics meets correlated electrons
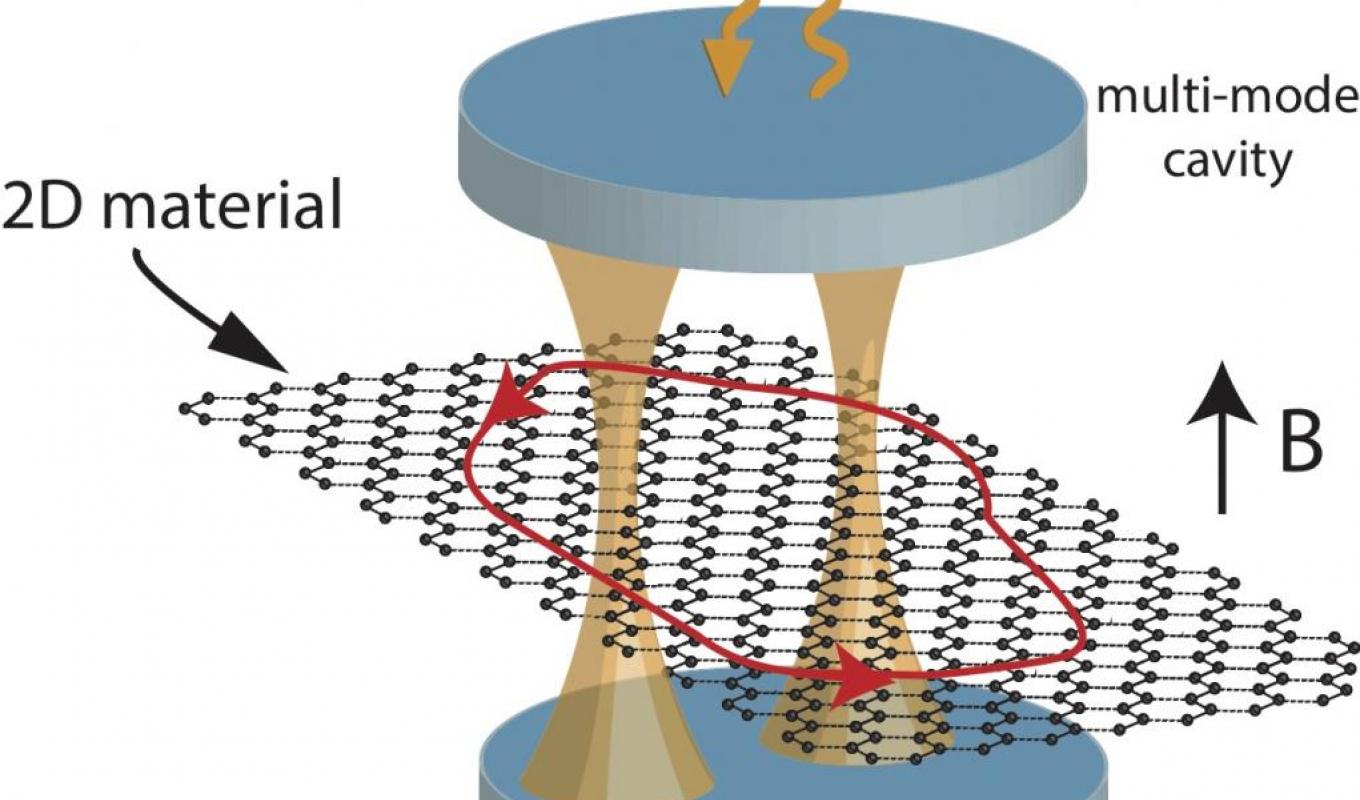
One of the key challenges in the development of quantum technologies is the control of light-matter interaction at the quantum level where individual excitations matter. During the past couple of decades, there has been tremendous progress in controlling individual photons and other excitations such as spin, excitonic, and phononic in solid-state systems. Such efforts have been motivated to develop quantum technologies such as quantum memories, quantum transducers, quantum networks, and quantum sensing. While these efforts have been mainly focused on control and manipulation of individual excitations (i.e., single-particle physics), both desired and undesired many-body effects have become important. Therefore, it is intriguing to explore whether these quantum optical control techniques could pave a radically new way to prepare, manipulate, and detect non-local and correlated electronic states, such as topological ones.
Machine Learning in quantum systems

Topological Photonics

Physicists classify and understand systems in terms of many properties; color, mass, length and microscopic symmetries are familiar examples. Another interesting feature is a system’s topology, or how its parts connect. As an example, a circular linked necklace can be deformed into an oval or a rectangle without changing the topology, since the links remain connected in the same way. But the necklace can only be made into the topologically distinct straight line if it is cut or its clasp is opened. In the 1980s physicists realized that some physical properties are entirely dictated by a system’s topology.